引言

在高性能的乱序执行处理器当中，为了尽可能的提高处理器的吞吐率，一个准确的分支预测器可以起到至关重要的作用：这是因为，在深流水线以及乱序处理的微处理器中，一条分支指令的预测错误会带来接近10个时钟周期甚至更多的冲刷惩罚，换句话说，从这条分支指令进行预测到BRU（Branch Unit，指专门处理分支指令的运算单元）发现错误这之间，所有比该条分支指令更年轻¹的指令都将会是无用功，而这可能已经设计到了几十条甚至上百条指令的取消，这个代价是非常大的。

为了尽可能的降低分支预测错误的次数，目前已经有相当多的分支预测算法被提出，在这一系列的文章中，笔者根据自身的理解来对这些分支预测算法进行介绍。需要注意的是，本系列文章将设定读者具有基本的分支预测算法了解，如果需要补充这方面的知识，可以阅读《计算机体系结构：量化研究方法》的附录C.2一节进行了解。

由于笔者水平所限，这其中也可能会有一些错误或者不足之处，恳请读者批评指正。

本系列文章目录

• 分支预测算法（一）：TAGE
• 分支预测算法（二）：Loop Predictor与Statistical Corrector
• 分支预测算法（三）：分支预测并非是已经解决的问题

TAGE²是现今最经典的分支预测算法，TAGE及其后续的变体都是当今高性能微处理器的分支预测算法基础。因此，要聊分支预测算法的话题必定绕不开TAGE。

TAGE的全称是 TAgged GEometric history length (predictor)，也就是基于带标签的几何级数递增历史长度的分支预测算法，其核心主要是两个部份：

1. 呈几何级数递增的分支历史长度匹配机制
2. 带标签的索引表项

TAGE预测器的基本组成为：

1. 一个基于bimodal³的直接索引预测表T₀（有时候也称为tagless table），用于在T_N表（tagged table）都无法命中时提供基本的预测。
2. 若干基于几何级数递增的分支历史长度进行部份匹配的索引表项T_N，带标签的意义在于其索引T_N表的方式在于将分支指令的地址与分支历史（一般来说是全局分支历史）进行哈希操作（也就是异或运算）后进行索引，并使用另一种PC与分支历史哈希操作得到的标签tag与对应索引表项的tag进行比对来决定是否命中。索引值与标签的哈希方式可以有多种不同的计算方式，将会在后日谈：TAGE在微架构的具体实现一章中进行讨论。

基于几何级数递增的分支历史长度预测

该策略在O-GEHL预测器⁴中提出，假设有M个预测表T_i（0 ≤ i < M），且每个表使用分支指令的地址与不同长度的全局分支历史的哈希值进行索引，每个表T_i匹配的全局分支历史长度服从几何级数递增：L(i) = (int)(a^i-1 * L(1))

使用基于几何级数递增的分支历史长度允许预测器在允许捕捉超长全局分支历史模式的同时，将大部份的存储资源分配给使用较短的分支历史长度进行匹配的表项。

TAGE预测器

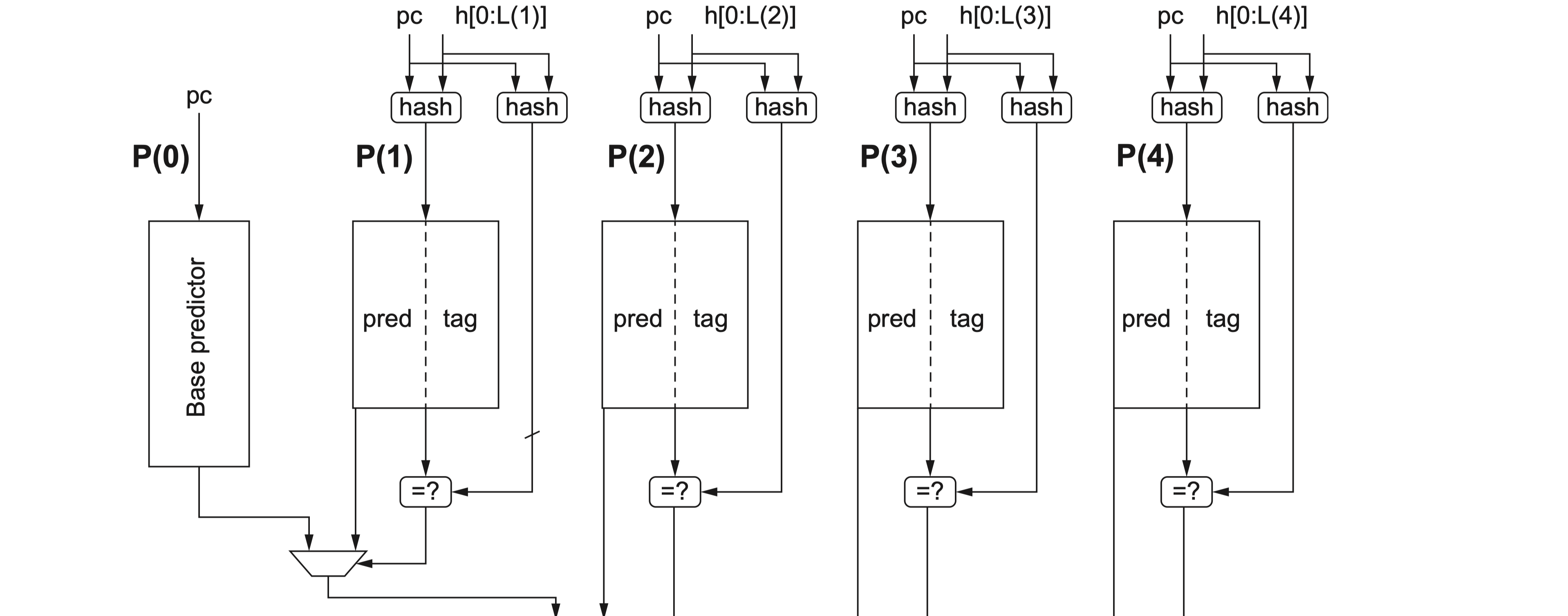
TAGE预测器的灵感来源于PPM-like（prediction partial matching）tag-based预测器⁵。图1是TAGE预测器的结构。

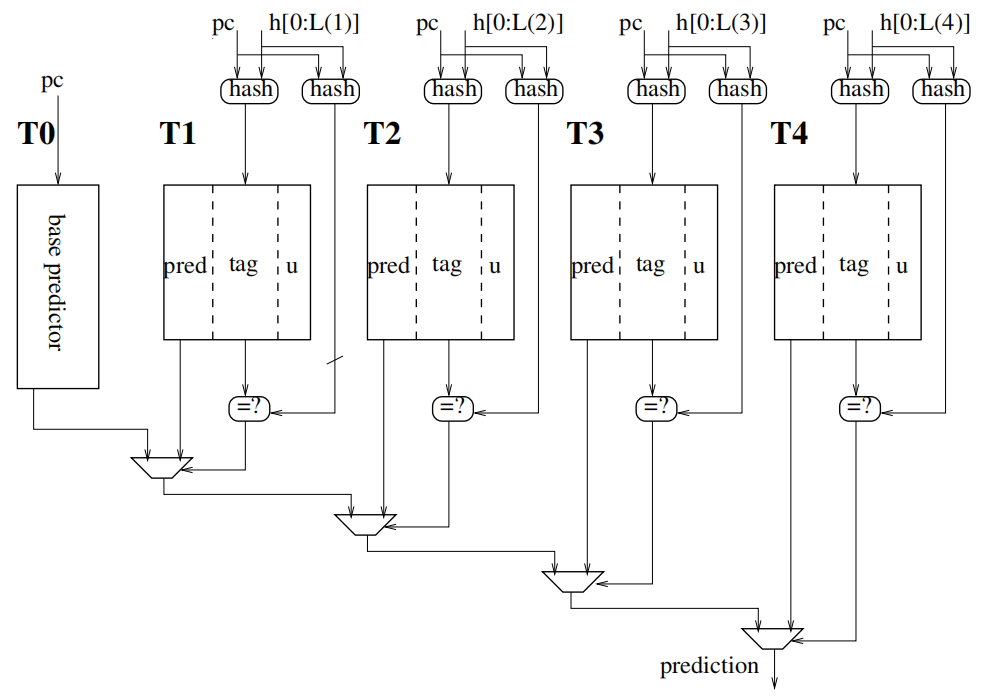
其中：

• T₀表是使用PC直接索引的2位饱和计数器组成的bimodal表项
• T_N表是使用PC与对应全局分支历史长度进行哈希索引的带标签表，其每个表项中：
  • pred：3位的有符号饱和计数器，符号位表示预测跳转与否，1表示预测跳转（taken），0表示预测不跳转（not-taken）
  • tag：PC与分支历史哈希得到的标签信息，不同T_N表的tag长度可以相同，也可以不同。
  • u：2位useful计数器，表示当前表项“有用”的程度。

这里对后续需要使用的一些术语/缩写进行定义：

• provider component，pcpn：最终提供预测信息的表项
• final pred， fpred⁶：最终提供的预测信息
• alternate prediction， altpred：若命中的表项≥2，则altpred为命中的次长历史长度表项（T₀永远命中，且历史长度视为0）；若仅命中T₀，则T₀的预测结果也是altpred。

预测结果的计算

TAGE预测器的预测计算方式其实很简洁：根据分支指令的PC以及全局分支历史长度信息并行索引T₀以及T_N，预测结果由命中tag的最长T_N表的pred计数器的符号位给出。如果没有命中T_N表，则由T₀表的2位bimodal预测器给出。

预测器的更新

更新useful计数器u

当altpred的预测结果与fpred不同时，需要更新pcpn的useful计数器u：

• 若fpred与最终的分支跳转⁷结果相同时，则pcpn.u递增1
• 若fpred与最终的分支跳转结果不同时，则pcpn.u递减1

需要注意，对useful计数器的更新操作遵循饱和计算，即若u=3，则递增1无作用；若u=0，则递减1无作用。

同时，useful计数器u还起到年龄计数器的作用，其MSB（bit-1）以及LSB（bit-0）会周期性的交替重置为0。原文中的周期设置为每256K个分支指令进行一次重置操作。

正确预测的更新

如果fpred与最终的分支跳转结果相同，则对应的pcpn.pred根据最终的分支预测结果进行更新：

• 若最终的分支跳转结果为taken，则pcpn.pred递增1
• 若最终的分支跳转结果为not-taken，则pcpn.pred递减1

同样，对pcpn.pred的更新遵循饱和计算操作。

错误预测的更新

如果fpred与最终的分支跳转结果不同，则需要执行以下操作：

1. 更新pcpn.pred，其更新操作与正确预测时的更新操作相同
2. 如果最终给出预测结果的表T_i（pcpn对应的表）不是使用最长全局分支历史信息的表（即i < M），则尝试往使用更长的全局分支历史信息的表上分配一个新的表项：
   • 首先，读取所有比T_i使用更长全局分支历史信息表索引得到的表项的useful计数器u的值
   • 如果不存在表k（i < k < M)，其索引得到的表项的useful计数器u的值为0，则所有比T_i使用更长的全局分支历史信息的表项的u值递减1
   • 如果存在一个表k（i < k < M），其索引得到的表项的useful计数器u的值为0，则分配到对应的表中
   • 如果有2个或以上的表，如T_j，T_k表（i < j < k < M）使用的全局分支历史长度都比T_i表长，且其索引得到的表项的u值都为0，则分配的表项优先级中，T_j > T_k⁸
3. 新分配表项的初始化：
   • 根据最终的分支跳转结果设置pred计数器为：
     • 若最终的分支跳转结果为taken，则pred=4（3'b100），弱跳转
     • 若最终的分支跳转结果为not-taken，则pred=3（3'b011），弱不跳转
   • tag初始化为对应分支指令的PC与全局分支历史长度的标签哈希算法得到的标签值
   • u初始化为0（即：strong not useful，强没用）

更新策略的深入探讨

1. 之所以每次错误预测，都只会分配一个且仅此一个表项，是为了最小化一些偶发性或者与分支历史不甚相关的分支指令占据过多的表项的现象。
2. useful计数器的作用机理：
   • 保证最近“有用”的表项不会被替换掉
   • 维护一种近似于伪LRU的替换策略
   • 初始化为0，是为了保证该表项在有效的提供准确的预测结果时才可以获得长时间逗留的资格；而为了防止发生乒乓替换的现象，分配的优先级仲裁可以防止该现象的发生。

改进策略：最长命中预测信心不足时的预测选择

某些时候，当最长命中表项的pred计数器表明，该预测结果信心不足时，altpred会拥有更准确的预测结果。当然，如何定义强信心以及弱信心也可以有多种不同的定义方式，比如可以定义仅3'b100以及3'b011为弱信心，其他都为强信心。当然，你也可以定义仅3'b111以及3'b000为强信心，其他都为弱信心。

静态策略

如果最长命中表项pcpn的预测信心为强，则选择最长命中表项的预测结果；否则，选择altpred为最终预测结果。

动态策略

使用一个有符号的USE_ALT_ON_NA计数器来作为一个动态的阈值，来决定当最长命中表项信心不足时，最终预测结果的选择方式。USE_ALT_ON_NA可以是单个计数器，也可以是一个计数器寄存器组，其使用分支指令的PC直接索引。当最长命中表项的预测信息不为弱且USE_ALT_ON_NA为负时，选择最长命中预测的结果，否则选择altpred。

当altpred与最终的分支结果相同时，USE_ALT_ON_NA递增，反之则递减。

后日谈：TAGE在微架构的具体实现

对面积以及时序要求的妥协

针对具有不同性能、功耗以及面积要求的微处理器设计，对TAGE的具体实现需要进行不同的调整。

理论上来说，更多的T_N表可以达到更准确的效果，但物理实现上，无限制的增加T_N表显然不可能：更多的T_N表项会带来更大的面积开销，且预测的逻辑时序也更难达到要求。由于TAGE表项的庞大，其都是使用SRAM来实现，因此其对时序的要求要比REG2REG的路径更为严格。此外，不断增加T_N表项所得到的性能收益会逐渐收敛而并非线性增加⁹。

因此，在真实的微架构实现中，TAGE的表的数量以及表的大小都值得设计者去进行仔细的tuning，除此之外，值得进行tuning的点还有：

• tag的长度
• T_N表使用的全局分支历史长度
• T₀表的大小
• 是否需要采用改进策略
  • 如果需要，改进策略的altpred使用方式（比如，香山为了时序要求，altpred默认使用T₀）
• …

T_N表索引与Tag哈希计算方式的选择

实际上，哈希的计算有很多种，可以选择PC截取对应的长度与全局分支历史进行哈希，也可以两者都使用折叠的方式进行哈希，并且折叠的方式可以是完整的PC，也可以是截取对应长度的PC进行折叠，等等。最终选择怎样的哈希算法，也同样可以通过建模分析得到。

TAGE更新在真实微架构下的延迟特性

一般来说，从一条分支指令进行预测到最后退休，这之间可以是几个时钟周期到几十个甚至上百个时钟周期不等。这里带来了几个问题：

全局分支历史的维护：是否需要包含预测分支指令的结果？

如果全局分支历史只有在分支指令退休时才更新，那么全局分支历史的信息将会变得非常滞后，这对于预测的准确性来说是致命的。因此，在真实的微架构下，设计者需要维护一套策略来保证全局分支历史可以包含预测分支指令的结果，并在预测错误时会滚到正确的状态。

TAGE表项的更新：SRAM的读写冲突以及更新信息的滞后性

上面提到过，真实的物理实现当中，TAGE的表项都是使用SRAM来实现的。不同于寄存器组，SRAM一般使用单端口的SRAM¹⁰。那么，你需要解决同一个时钟周期读写冲突的情况。当然，你可以通过使用分块的SRAM bank来缓解冲突的问题，但这样会带来额外的面积开销。

如果你决定写（更新）比读（预测）具有更高的优先级，那么，预测的吞吐率将会降低。如果你决定读比写具有更高的优先级，那么，更新操作将会滞后，且预测根据的信息也将会变得陈旧，并且，更新的信息也会变得滞后，这里可以留作读者进行思考（实际上是笔者写累了）。香山对于这种情况则是使用了一个bypass的更新策略进行merge update，可以详见笔者的香山源码浅析：TAGE一文。