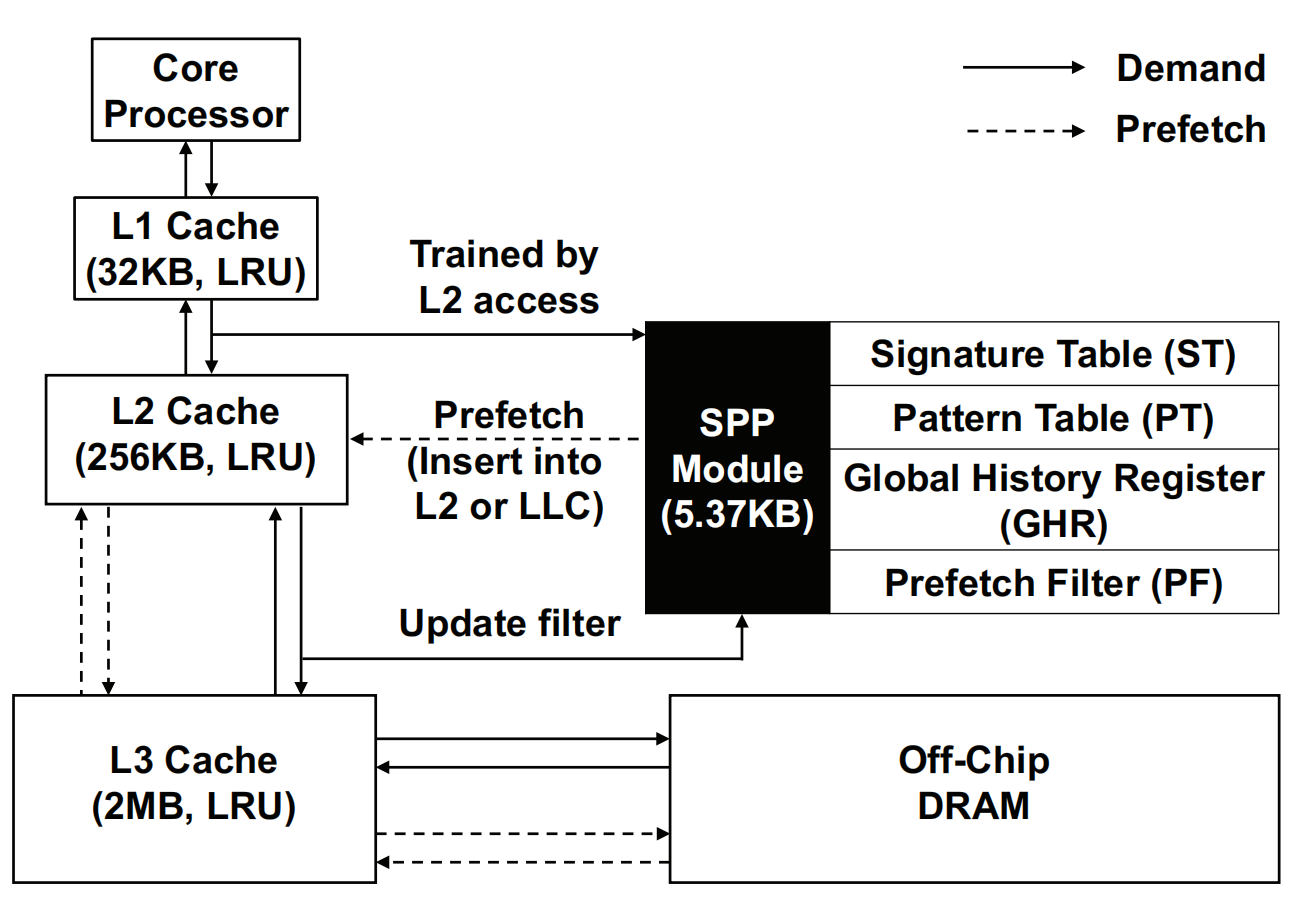
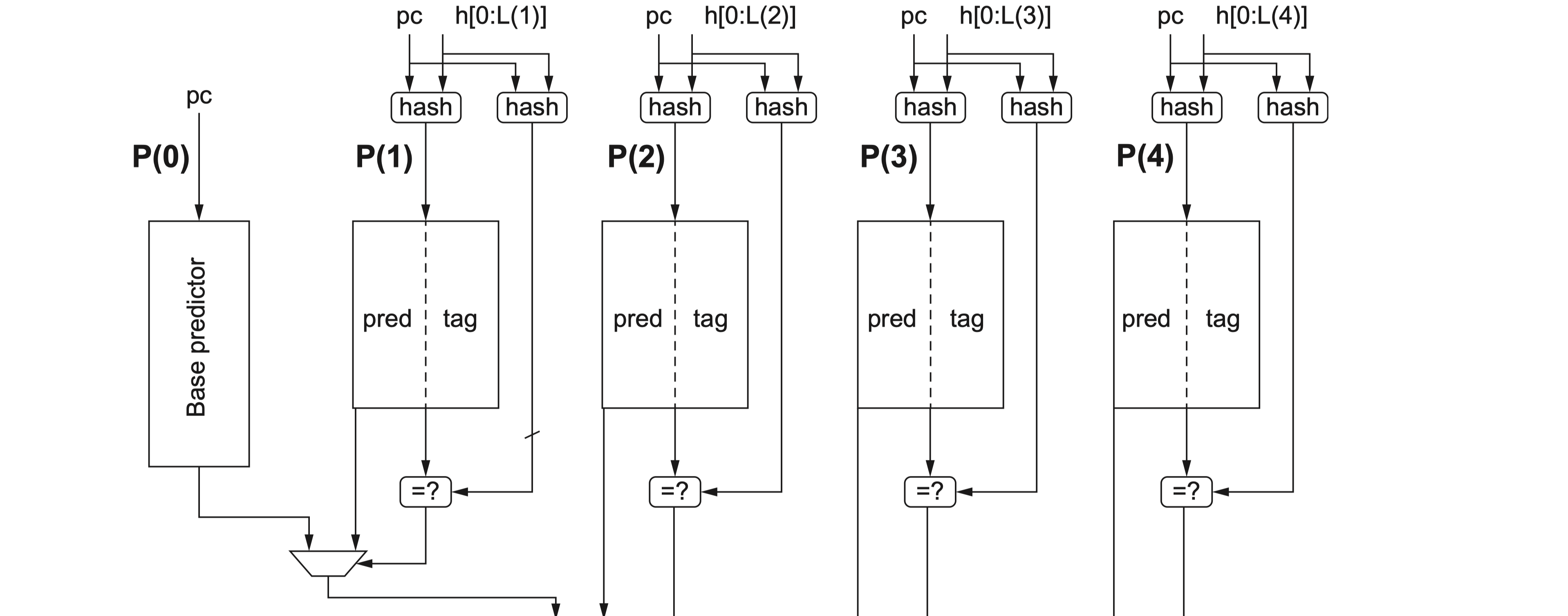
上一篇文章中介绍了TAGE预测器的基本结构以及算法,本文将会介绍TAGE的两种主要的变体,或者说是辅助预测器件,即Loop Predictor(“L”)以及Statistical Corrector(“SC”)。对应的TAGE预测器变体则可以是TAGE-L/TAGE-SC/TAGE-SC-L。本文所参考的论文主要为:
- Seznec, A. (2011, December). A new case for the tage branch predictor. In Proceedings of the 44th Annual IEEE/ACM International Symposium on Microarchitecture (pp. 117-127).
- Seznec, A. (2014, June). Tage-sc-l branch predictors. In JILP-Championship Branch Prediction.
- Seznec, A. (2016). Tage-sc-l branch predictors again. In 5th JILP Workshop on Computer Architecture Competitions (JWAC-5): Championship Branch Prediction (CBP-5).
Loop Predictor
对于具有固定迭代次数的循环来说,其循环出口的判断对应的分支指令一般只与自身的局部历史信息相关,即循环常数次后将会退出循环体(也就是需要给出常数次后相反的跳转方向)。如果循环内的分支行为具有规律或比较常规,那么TAGE一般都可以捕捉到该循环出口判断的分支指令跳转行为。然而,当循环内的控制流比较混乱或不具有规律时,TAGE则很难准确预测到循环退出的时间点。
Loop Predictor的作用就是用于捕捉并记录具有固定迭代次数的循环,并在该循环反复执行多次后,在Loop Predictor中的记录项达到“强信心”的状态时,给出退出时刻的预测1。
Loop Predictor由多个记录固定迭代次数循环的entry构成。Loop Predictor一般会设计只具有有限的大小以及高度的相联性2。每个entry包含:(总计39-bits)
- past iteration count:已经经过的循环次数,一般为10-bits
- retire iteration count:循环需要执行的个数,也就是循环退出(retire)所经过的迭代次数,一般为10-bits
- partial tag:循环标签,一般通过PC哈希得到,一般为10-bits
- confidence counter:信心计数器,一般为4-bits
- age counter:年龄计数器,一般为4-bits
- direction bit:标志循环跳转的方向,1-bit
Age counter
替换:Loop Predictor的替换策略基于age counter,当一个entry的age counter为0时,其可以被替换。
分配:一个entry被分配时,其age counter初始化为7。
更新:当一个entry是潜在的被替换对象时,age counter递减。当一个entry给出准确的预测时,age counter递增。当一个entry中的循环不再认为是一个普通的循环时,age counter直接置为0。
实现方案
在论文原文中,实际上有一些实现的细节并没有做说明,这里给出一种可能的Loop Predictor实现方案,该实现方案基于TAGE并加入Loop Predictor进行矫正,即TAGE-L预测器:
-
一个Loop Predictor的动态阈值计数器
wtl_cnt,范围是 -255 ≤wtl_cnt≤ 127。当Loop Predictor中命中的entry有效(confidence counter=0xF)时进行更新,若TAGE-L最终给出的预测正确,则递增,否则递减。 -
Loop Predictor中每个entry的结构:
- pastiter:10-bits,记录当前entry对应的循环已经执行的次数。当预测器遇到当前entry对应的分支指令时,递增。
- retireiter:10-bits,记录当前entry对应的循环应该要执行的次数。若当前pastiter≠0且retireiter=0,entry对应的分支指令的实际跳转方向与dir不同时,设置为pastiter的值。若发生预测错误,则直接重置为0。
- confidence:4-bits,记录当前entry对应的循环是否有效。若dir与当前实际跳转方向不同,且pastiter=retireiter时,递增。当预测错误时,直接重置为0。
- age:4-bits,用于替换算法。若当前entry对应的循环有效,且其给出的预测结果正确并与TAGE给出的预测结果不同时,递增。当预测错误时,直接重置为0。
- dir:1-bit,记录当前循环退出分支,在不退出循环时的跳转方向。
-
分配策略:当TAGE预测错误时,尝试在Loop Predictor中分配一个entry。从潜在可分配的entry中随机选择一个entry,若其age为0,则分配到该entry;否则,该entry的age递减。当分配一个entry时,其age初始化为7,confidence、pastiter、retireiter初始化为0。
The Statistical Corrector Predictor
TAGE在预测具有相关性的分支指令上具有非常高的准确率,即使其相关性分散在非常长的全局分支历史当中(如接近1k条分支指令)。但TAGE在预测不具有相关性的具有静态偏置性质的分支上效果则很糟糕,甚至不如使用PC直接索引的具有更宽的饱和计数器效果来的好。
而为了更好的预测这类分支指令,在TAGE中引入了Statistical Corrector(后文都简称为“SC”)Predictor。SC的目的是为了检测TAGE对于这些指令所做出的不太可能正确的预测并矫正它们:SC结合TAGE的预测、地址以及分支历史来决定是否需要矫正TAGE的预测结果。同时,由于大多数TAGE所做出的预测都是正确的,因此大部分情况下,SC都不会纠正TAGE的预测结果,因此相对有限大小的SC与无限大小的SC所表现的性能并没有太大的差异。
SC基本设计理念
SC算法的灵感来自于GEHL预测器3。SC由若干个使用PC、不同长度的分支历史(如0、6、10、17bit)以及TAGE的预测结果进行索引的表构成,而每个表项则是1个6-bits的有符号饱和计数器。
SC的预测结果基于以下的计算原则:
- 计算索引得到的表中所有有符号计数器的centered4后的求和值sum1
- 将TAGE预测的计数器值ctrTAGE进行centered并乘以8,与sum1相加得到sum2,即sum2=sum1+8*(2*ctrTAGE+1)。这么做的原因是,可以将TAGE中的confidence信息也考虑到最终预测结果的计算当中
- sum2的符号位即为SC的预测结果
- SC的预测结果矫正TAGE的预测结果的条件是:SC的预测结果与TAGE的预测结果相反,且|sum2|大于等于一个动态的阈值,这个动态的阈值将会在执行过程中动态的调整来保证SC所做出的预测较为有效。
有限大小下SC的设计:The Corrector Filter
在较为有限面积资源的限制下,大部份资源都将会被TAGE本体所占有。因此,这种情况下SC可以实现为一个具有相联性的表,称为矫正过滤器,用于记录TAGE预测错误的分支指令。TAGE每次的预测错误分支指令的PC以及预测的方向都会以较低的概率记录进入该表中。当命中SC时,如果其矫正的信心足够高,则会矫正TAGE的预测结果。替换的策略则是倾向于弱信心的表项。
具体来说,你可以将SC设计成一个64-entry、2路组相联的表,每个表项带有6-bits的饱和计数器以及7-bits的tag。一种可能的优化策略是:TAGE所做出的强信心的预测,则更倾向于不会被矫正。
中至大型面积资源下SC的设计:Multi-GEHL Statistical Corrector Predictor
在更多的面积资源下,可以使用更多的表项来设计SC,即Multi-GEHL SC predictor(MGSC),其包含6个不同的组件:
- Bias component:使用PC以及TAGE的预测结果进行索引。包含2个表,并使用不同的哈希算法进行索引。
- 5 GEHL-like components:
- 使用全局分支历史索引的4个表
- 使用RAS5关联分支历史索引的4个表(用于捕捉一些函数调用中的相关性)
- 3个256-entry的局部历史表
- 16-entry的局部历史表(有2个使用不同哈希函数索引的component,一个4个表另一个3个表)
每个表项中索引得到的计数器的位宽可以是5位或者6位。预测的计算方式与上面提到的计算原则相同,此外,还可以额外加上MGSC表项数*2并乘以跳转方向(+1,-1)的结果作为最终的SC预测结果。
此外,还存在一种改进的策略来进一步提升SC预测的准确性。当TAGE的预测结果为强信心且MGSC的预测结果为弱信心时(|sum| < threshold),TAGE的预测结果要更为准确。如果还要追求更为极致的性能,还可以对MGSC的弱信心预测结果划为三档:极弱信心(very low,|sum| < threshold/3)、中度弱信心(medium low,threshold/3 < |sum| < 2*threshold/3)以及轻度弱信心(high low,2*threshold/3 < |sum| < threshold),并分别维护3个独立的阈值来控制最后是否选择MGSC的预测结果。
实现方案
由于论文中提到的SC相关的实现方案实在是比较多样且复杂,这里给出一种可行的SC实现方案:
SC中包含有4个component,分别为:
- Global Component,GSC:具有4个表,1K-entry,使用6-bits的有符号计数器。使用PC、TAGE预测结果以及不同的长度的全局分支历史来进行索引。当分支最终跳转时+1,否则-1。
- Local Component,LSC:具有4个表,1K-entry,使用6-bits的有符号计数器。使用PC、TAGE预测结果以及不同长度的局部分支历史来进行索引。当分支最终跳转时+1,否则-1。
- Bias Component:具有2个表,128-entry,使用6-bits的有符号计数器。使用PC以及TAGE预测结果哈希索引。当分支最终跳转时+1,否则-1。
- SC Threshold Component:具有1个表,32-entry,使用8-bits的无符号计数器。使用PC进行索引。当SC的预测结果错误时+1,否则-1。
上面提到所有表的更新条件为:SC预测结果错误或者SC求和结果的绝对值比读取的阈值要小。
最后,一个TAGE-SC-L预测器的结构图如下所示:

后日谈:SC在真实微架构下的设计取舍
SC实现的灵活性
实际上,SC的实现具有相当的灵活性,因此其对于建模团队来说是不小的挑战。因此,SC结合不同的微处理器性能、面积以及功耗的需求,有相当多可以进行tuning的点:
- 表项的大小
- 有符号计数器的宽度
- 全局历史、局部历史的长度
- 各改进策略是否实施
- ……
并且,在实际的微架构实现当中,TAGE-SC-L实现的时序压力非常大,特别是在高频率的设计当中(当然,你需要用到TAGE-SC-L的必然是性能要求比较高的微处理器,其频率也不会低到哪里去)。因此,对于TAGE-SC-L的预测所需要的stage也需要精心设计。
SC与神经网络?
实际上,SC的预测方式就像是一个单层的神经网络。其实SC就是perceptron预测器6的一种变体,每个有符号计数器就是一个神经元中的权重,并根据最终分支的真实预测结果进行训练并更新其权重。
在论文原文中,这个值设定为7次,也就是一个固定迭代次数的循环执行7次后,即达到“强信心”状态。 ↩︎
在论文原文中,Loop Predictor设计为具有64个entry及4路组相联的结构。 ↩︎
Seznec, A. (2005, June). Analysis of the o-geometric history length branch predictor. In 32nd International Symposium on Computer Architecture (ISCA’05) (pp. 394-405). IEEE. ↩︎
即读取得到的计数器值
ctr,centered后的值为:2*ctr+1 ↩︎Return Address Stack,即返回地址栈。每次遇到一条call指令时,就会将其返回地址(也就是call地址的下一个地址)压入RAS中。 ↩︎
Jiménez, D. A., & Lin, C. (2001, January). Dynamic branch prediction with perceptrons. In Proceedings HPCA Seventh International Symposium on High-Performance Computer Architecture (pp. 197-206). IEEE. ↩︎